Number
Get Widget Get link Report a Bug Save result Print Today calculations: 0

Table of contents:

  1. Prime Factorization Calculator
  2. What is Prime Factorization?
  3. A factor tree method
  4. Prime Factorization of a Number List
  5. References

This Prime Factorization Calculator to find all prime factors of a given integer number. This calculator presents:

  • all prime factors of a number,
  • prime decomposition in exponential form,
  • comma separated list of prime factors (CSV format),
  • all factors of a number,
  • prime factors tree.

What is Prime Factorization?

The process of writing a number as the product of prime numbers is prime factorization.

Factorization of prime numbers is finding prime numbers, multiplying which you can get the original number.

Example: find the prime factors of 36

Prime factorization is a way of expressing a number as a product of its prime factors. The smallest prime factor of 36 is 2.

  • Step 1: 36 ÷ 2 = 18, save 2.
  • Step 2: 18 ÷ 2 = 9, save 2.
  • Step 3: 9 is not completely divisible by 2. Next prime factor of 36 is 3. 9 ÷ 3 = 3, save 3.
  • Step 4: 3 is only divisible by itself and 1, so it is a prime number. Save 3.
  • Result: Therefore, the prime factorization of 36 is expressed as 2 × 2 × 3 × 3 (or 22 × 32 in exponential form). 2 and 3 are prime numbers and the prime factors of 36 – Check in Factoring Calculator.

A factor tree method

We will use the factorization of number to draw the factor trees.

Example: find the prime factors of 60

We can also find the prime factors of 60 using a factor tree. The factor tree of 60 can be drawn by factorizing 60 until we reach its prime factors.

  • Step 1: Split 60 into two any factors. Let us take 2 and 30.
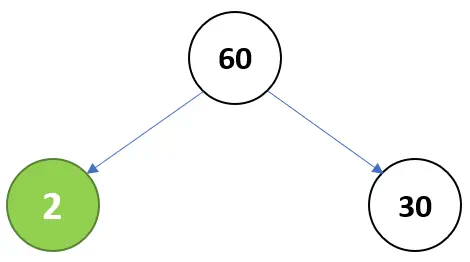
    factor tree of 60 (step 1)
    2 is a prime number we green circle it as one of the prime factors of 60. 30 is a composite number and further split it into many factors. We repeat the process of factorizing the composite numbers and splitting it into branches until we reach a prime number.
  • Step 2: Split 30 into two any factors. Let us take 2 and 15.
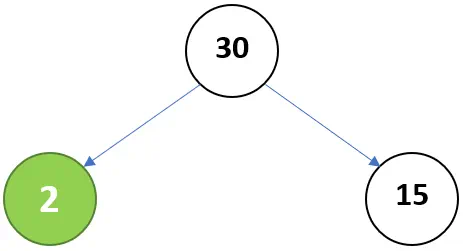
    factor tree of 60 (step 2)
    Circle the number 2 in green because it is a prime number.
  • Step 3: Split 15 into 3 and 5.
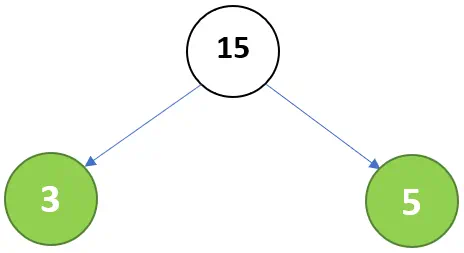
    factor tree of 60 (step 3)
    Circle the number 3 and 5 in green because it is a prime number.
  • Result: The prime factors of 60 = 2 × 2 × 3 × 5 – Check in Factoring Calculator.
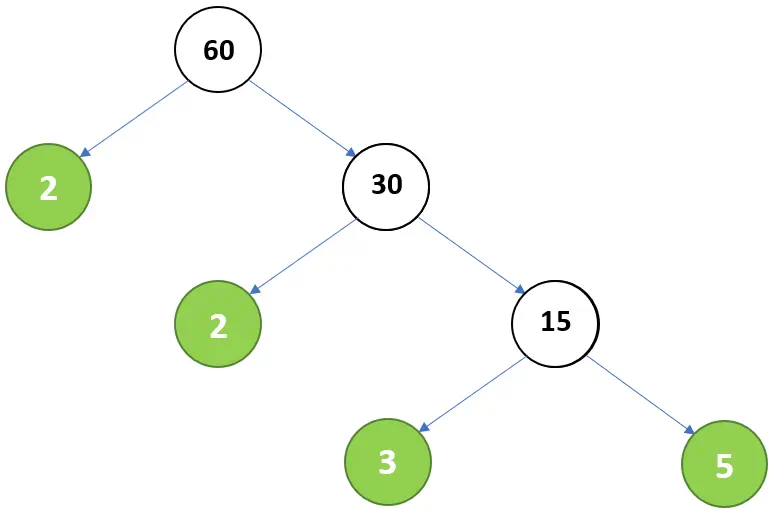
    factor tree of 60 (result)

Prime Factorization of a Number List

  • Prime factorization of 2: it’s a prime number!
  • Prime factorization of 3: it’s a prime number!
  • Prime factorization of 4: 2 × 2, or 22
  • Prime factorization of 5: it’s a prime number!
  • Prime factorization of 6: 2 × 3
  • Prime factorization of 7: it’s a prime number!
  • Prime factorization of 8: 2 × 2 × 2, or 23
  • Prime factorization of 9: 3 × 3, or 32
  • Prime factorization of 10: 2 × 5
  • Prime factorization of 11: it’s a prime number!
  • Prime factorization of 12: 2 × 2 × 3, or 22 × 3
  • Prime factorization of 13: it’s a prime number!
  • Prime factorization of 14: 2 × 7
  • Prime factorization of 15: 3 × 5
  • Prime factorization of 16: 2 × 2 × 2 × 2, or 24
  • Prime factorization of 17: it’s a prime number!
  • Prime factorization of 18: 2 × 3 × 3, or 2 × 32
  • Prime factorization of 19: it’s a prime number!
  • Prime factorization of 20: 2 × 2 × 5, or 22 × 5
  • Prime factorization of 21: 3 × 7
  • Prime factorization of 22: 2 × 11
  • Prime factorization of 23: it’s a prime number!
  • Prime factorization of 24: 2 × 2 × 2 × 3, or 23 × 3
  • Prime factorization of 25: 5 × 5, or 52
  • Prime factorization of 26: 2 × 13
  • Prime factorization of 27: 3 × 3 × 3, or 33
  • Prime factorization of 28: 2 × 2 × 7, or 22 × 7
  • Prime factorization of 29: it’s a prime number!
  • Prime factorization of 30: 2 × 3 × 5
  • Prime factorization of 31: it’s a prime number!
  • Prime factorization of 32: 2 × 2 × 2 × 2 × 2, or 25
  • Prime factorization of 33: 3 × 11
  • Prime factorization of 34: 2 × 17
  • Prime factorization of 35: 5 × 7
  • Prime factorization of 36: 2 × 2 × 3 × 3, or 22 × 32
  • Prime factorization of 37: it’s a prime number!
  • Prime factorization of 38: 2 × 19
  • Prime factorization of 39: 3 × 13
  • Prime factorization of 40: 2 × 2 × 2 × 5, or 23 × 5
  • Prime factorization of 41: it’s a prime number!
  • Prime factorization of 42: 2 × 3 × 7
  • Prime factorization of 43: it’s a prime number!
  • Prime factorization of 44: 2 × 2 × 11, or 22 × 11
  • Prime factorization of 45: 3 × 3 × 5, or 32 × 5
  • Prime factorization of 46: 2 × 23
  • Prime factorization of 47: it’s a prime number!
  • Prime factorization of 48: 2 × 2 × 2 × 2 × 3, or 24 × 3
  • Prime factorization of 49: 7 × 7, or 72
  • Prime factorization of 50: 2 × 5 × 5, or 2 × 52
  • Prime factorization of 51: 3 × 17
  • Prime factorization of 52: 2 × 2 × 13, or 22 × 13
  • Prime factorization of 53: it’s a prime number!
  • Prime factorization of 54: 2 × 3 × 3 × 3, or 2 × 33
  • Prime factorization of 55: 5 × 11
  • Prime factorization of 56: 2 × 2 × 2 × 7, or 23 × 7
  • Prime factorization of 57: 3 × 19
  • Prime factorization of 58: 2 × 29
  • Prime factorization of 59: it’s a prime number!
  • Prime factorization of 60: 2 × 2 × 3 × 5, or 22 × 3 × 5
  • Prime factorization of 61: it’s a prime number!
  • Prime factorization of 62: 2 × 31
  • Prime factorization of 63: 3 × 3 × 7, or 32 × 7
  • Prime factorization of 64: 2 × 2 × 2 × 2 × 2 × 2, or 26
  • Prime factorization of 65: 5 × 13
  • Prime factorization of 66: 2 × 3 × 11
  • Prime factorization of 67: it’s a prime number!
  • Prime factorization of 68: 2 × 2 × 17, or 22 × 17
  • Prime factorization of 69: 3 × 23
  • Prime factorization of 70: 2 × 5 × 7
  • Prime factorization of 71: it’s a prime number!
  • Prime factorization of 72: 2 × 2 × 2 × 3 × 3, or 23 × 32
  • Prime factorization of 73: it’s a prime number!
  • Prime factorization of 74: 2 × 37
  • Prime factorization of 75: 3 × 5 × 5, or 3 × 52
  • Prime factorization of 76: 2 × 2 × 19, or 22 × 19
  • Prime factorization of 77: 7 × 11
  • Prime factorization of 78: 2 × 3 × 13
  • Prime factorization of 79: it’s a prime number!
  • Prime factorization of 80: 2 × 2 × 2 × 2 × 5, or 24 × 5
  • Prime factorization of 81: 3 × 3 × 3 × 3, or 34
  • Prime factorization of 82: 2 × 41
  • Prime factorization of 83: it’s a prime number!
  • Prime factorization of 84: 2 × 2 × 3 × 7, or 22 × 3 × 7
  • Prime factorization of 85: 5 × 17
  • Prime factorization of 86: 2 × 43
  • Prime factorization of 87: 3 × 29
  • Prime factorization of 88: 2 × 2 × 2 × 11, or 23 × 11
  • Prime factorization of 89: it’s a prime number!
  • Prime factorization of 90: 2 × 3 × 3 × 5, or 2 × 32 × 5
  • Prime factorization of 91: 7 × 13
  • Prime factorization of 92: 2 × 2 × 23, or 22 × 23
  • Prime factorization of 93: 3 × 31
  • Prime factorization of 94: 2 × 47
  • Prime factorization of 95: 5 × 19
  • Prime factorization of 96: 2 × 2 × 2 × 2 × 2 × 3, or 25 × 3
  • Prime factorization of 97: it’s a prime number!
  • Prime factorization of 98: 2 × 7 × 7, or 2 × 72
  • Prime factorization of 99: 3 × 3 × 11, or 32 × 11
  • Prime factorization of 100: 2 × 2 × 5 × 5, or 22 × 52
  • Prime factorization of 120: 2 × 2 × 2 × 3 × 5, or 23 × 3 × 5
  • Prime factorization of 144: 2 × 2 × 2 × 2 × 3 × 3, or 24 × 32
  • Prime factorization of 150: 2 × 3 × 5 × 5, or 2 × 3 × 52
  • Prime factorization of 180: 2 × 2 × 3 × 3 × 5, or 22 × 32 × 5
  • Prime factorization of 200: 2 × 2 × 2 × 5 × 5, or 23 × 52
  • Prime factorization of 225: 3 × 3 × 5 × 5, or 32 × 52
  • Prime factorization of 300: 2 × 2 × 3 × 5 × 5, or 22 × 3 × 52
  • Prime factorization of 343: 7 × 7 × 7, or 73
  • Prime factorization of 360: 2 × 2 × 2 × 3 × 3 × 5, or 23 × 32 × 5
  • Prime factorization of 441: 3 × 3 × 7 × 7, or 32 × 72
  • Prime factorization of 512: 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, or 29
  • Prime factorization of 529: 23 × 23, or 232
  • Prime factorization of 625: 5 × 5 × 5 × 5, or 54
  • Prime factorization of 675: 3 × 3 × 3 × 5 × 5, or 33 × 52
  • Prime factorization of 729: 3 × 3 × 3 × 3 × 3 × 3, or 36
  • Prime factorization of 841: 29 × 29, or 292
  • Prime factorization of 980: 2 × 2 × 5 × 7 × 7, or 22 × 5 × 72
  • Prime factorization of 1000: 2 × 2 × 2 × 5 × 5 × 5, or 23 × 53

References

  1. Integer factorization (Wikipedia)

Page views: 1043