log of
with base
  • 2
  • e
  • 10
Get Widget Get link Report a Bug Save result Print Today calculations: 0

Table of contents:

  1. Log Calculator
  2. What is a Logarithm?
  3. Laws of Logarithms
  4. FAQ
  5. Conclusion

Logarithms are fundamental mathematical tools used to solve exponential equations, analyze growth rates, and transform complex calculations into simpler forms. A log calculator simplifies the process of evaluating logarithmic expressions, making it essential for various fields. In this in-depth guide, we’ll explore logarithms, the significance of log calculators, real-world applications, calculations, formulas, and answers to frequently asked questions.

What is a Logarithm?

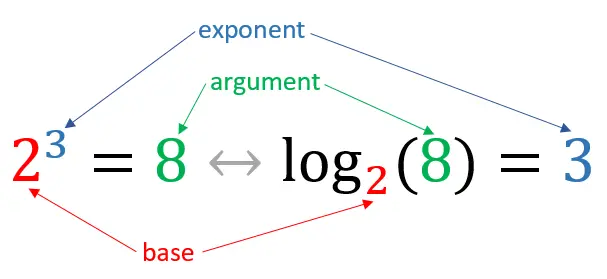
Logarithms are the inverse operations of exponentials. The logarithm base ‘b’ of a number ‘x’ is denoted as \log_b(x) = y, representing the exponent to which ‘b’ must be raised to obtain ‘x’. Mathematically, \log_b(x) = y can be rewritten as b^y = x

logb(x) = y ⟺ by = x

Both equations describe the same relationship between a, b and c:

  • b is the base,
  • y is the exponent, and
  • x is called the argument.

logarithm and exponent

Manual logarithmic calculations can be time-consuming and prone to errors. A log calculator simplifies this process, enabling you to quickly evaluate logarithmic expressions for any base and argument.

Logarithms find applications in diverse fields. In finance, they help calculate compound interest and growth rates. In science, they aid in measuring the intensity of earthquakes and the pH of solutions. In computer science, they are used to analyze algorithms’ time complexity.

Evaluating logarithms manually involves finding the exponent ‘y’ that, when raised to the base ‘b’, equals the given number ‘x’. For instance, \log_2(8) = 3 because 2^3 = 8

Exponential form Logarithmic form
23 = 8 log2(8) = 3
54 = 625 log5(625) = 4
52 = 25 log5(25) = 2

Logarithmic transformations are used to normalize data distributions, making them suitable for statistical analysis. Logarithmic scales are also employed in graphs to visualize exponential growth or decay patterns.

Laws of Logarithms

Product Rule \log_b(mn) = \log_b(m) + \log_b(n)
Quotient Rule \log_b(\frac{m}{n}) = \log_b(m) – \log_b(n)
Power Rule \log_b(n^p) = p \log_b(n)
Zero Rule \log_b(1) = 0
Identity Rule \log_b(b) = 1
Log of Exponent Rule \log_b(b^k) = k
Exponent of Log Rule b ^ {\log_b(k)} = k
Root Rule \log_b(\sqrt[q]{n}) = \frac{1}{q} \log_b(n)
Change of base Rule \log_b(n) = {\log_a(n)}/{\log_a(b)}

FAQ

Can logarithms be negative?

Logarithms are defined for positive numbers; however, their values can be negative.

What’s the relationship between logarithms and exponential functions?

Logarithms and exponentials are inversely related functions.

How does a log calculator handle different bases?

A log calculator can evaluate logarithms for various bases, providing accurate results.

Are there real-world instances where logarithms are used to simplify calculations?

Yes, logarithms are frequently used to simplify complex calculations involving large numbers or exponential growth.

Conclusion

Logarithms play a pivotal role in simplifying mathematical calculations, finding applications across science, finance, and technology. A log calculator empowers you to quickly evaluate logarithmic expressions, enhancing problem-solving capabilities. Understanding logarithms’ properties and applications offers insights into their broad significance across various domains.

Page views: 2787