Annulus Sector Area
Last updated: April 11, 2023
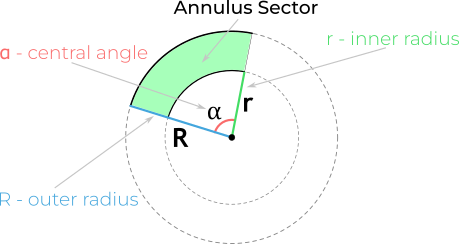
An annulus sector is a portion of a circle that is bounded by the inner arc of a given ring, the outer arc of a given ring, and two outer radii of the given ring.
Calculating the area of an annulus sector can be done using a simple formula, which involves the radius of the outer and inner circles and the central angle of the circle.
To begin, let’s define the terms involved in the calculation of the area of an annulus sector. The radius of a circle is the distance from the center of the circle to any point on its circumference. An annulus is a ring-shaped area between two concentric circles, where the outer radius is larger than the inner radius. The central angle is the angle formed by two radii that originate from the center of the circle and intersect at any point on its circumference.
The radius of the outer circle will call R, the radius of the inner circle we’ll call r and the angle between the radii is alpha (α).
Annulus Sector Area Formula
To get the annulus sector area use the formula:
- if the angle α is in degrees:
{A = \pi \cdot \dfrac{\alpha \degree}{ 360 \degree} \cdot(R^2 – r^2)}
- if the angle α is in radians:
{A = \dfrac{\alpha}{ 2} \cdot(R^2 – r^2)}
where A is the area of the annulus sector,
R is the outer radius of the annulus,
r is the inner radius of the annulus,
α is the central angle in degrees (or radians),
and π is a mathematical constant, approximately equal to 3.14.
Annulus Sector Area Examples
Here are some examples of how to calculate the annulus sector area:
Example 1
Let’s use an example to illustrate how to use this formula to calculate the area of an annulus sector. Suppose we have an annulus with an outer radius of 8 centimeters, an inner radius of 4 centimeters, and a central angle of 90 degrees.
Solution
To find the area of the annulus sector, we need to substitute these values into the formula as follows:
A = (π/360) x (8^2 – 4^2) x 90
A = (3.14/360) x (64 – 16) x 90
A = (0.0087) x (48) x 90
A = 37.58 cm²
Therefore, the area of the annulus sector is 37.58 square centimeters.
Example 2
Find the area of an annulus sector with an outer radius of 6 cm, an inner radius of 4 cm, and a central angle of 45 degrees.
Solution
A = ((π x 45) / 360) x (6^2 – 4^2) = (π / 8) x (20) ≈ 7.85 cm²
Annulus sector area = (1/8) x 62.83 ≈ 7.85 cm²
Therefore, the area of the annulus sector is approximately 7.85 cm².
Example 3
Find the area of an annulus sector with an outer radius of 10 cm, an inner radius of 8 cm, and a central angle of 120 degrees.
Solution
A = ((π x 120) / 360) x (10^2 – 8^2) = (π / 3) x (100 – 64) = (π / 3) x (36) = 12 x π ≈ 37.68 cm²
Annulus sector area = (1/3) x 113.10 ≈ 37.68 cm²
Therefore, the area of the annulus sector is approximately 37.68 cm².
Conclusion
These are just a couple of examples, but you can use the same formula to calculate the area of any annulus sector.
It is important to note that the angle used in the formula should be in degrees. If the angle is given in radians, it needs to be converted to degrees before using the formula. To convert an angle in radians to degrees, you can use the following formula:
α (in degrees) = α (in radians) x (180/π)
where α is the angle in radians.
In conclusion, calculating the area of an annulus sector is a simple process that involves using a formula that includes the radius of the outer and inner circles and the central angle of the circle. By understanding this formula and using it correctly, you can easily calculate the area of any annulus sector, making it a useful tool for many mathematical and geometrical applications.
Page views: 1754